天津大学 程思涵 田喆 吴霞
【摘 要】服务业消耗能源比例日渐提高,服务部门的大部分能源用于办公建筑取暖、照明、计算和餐饮。办公用电又是办公建筑能耗的重要组成部分,因此,建立高精度的电负荷曲线模型至关重要。本文利用马尔科夫链蒙特卡洛方法,通过转移概率矩阵建立人员模型,得到有效用电人数;结合统计调研数据,利用不同电器不同时刻不同功率的使用概率,建立了电器模型。结合人员模型和电器模型,通过自下而上的建模思想得到日负荷曲线分布。所建模型具有系统性和通用性,仿真与实测对比分析验证了本文模型的可行性与准确性。
【关键词】自下而上,马尔科夫链,蒙特卡洛,电负荷
0 引言
近年来,我国经济水平飞速发展,建筑能耗水平也随之不断增长,办公建筑能耗作为我国建筑能耗的重要组成部分,其中电能占了很大比例。随着社会经济发展,办公用电仍有很大增长空间[1]。同时,办公建筑日负荷曲线的获取有利于推进智能电网、需求响应等技术的发展[2,3]。因此办公建筑日负荷曲线建模很有必要。
目前,有两种常用的电负荷曲线建模方法:一种是统计的方法,另一种是自下而上的方法。在统计方法中,研究对象是基于一组测量的负荷曲线,用其来描述输入数据的特征,然后根据提取的特征制定负荷模型[4];而在自下而上的方法中,终端电器是研究对象,重点是各个终端电器的使用模式制定,并以此得到总用电量[5,6]。
关于统计建模方法,文献[7]采用时变多元回归模型来进行电负荷建模,作者考虑到用户行为和公用事业生产效率变化,可以得到小时级的负荷曲线结果。王等人[8]提出了一种分解方法,通过分解测量数据以提取不同时间尺度(如季节和工作日)模式,进而模拟电力需求趋势。斯蒂芬等人[9]假设电力负荷服从非平稳多元高斯分布,进而提出了一个分析国内能源客户消费习惯的框架。关于自下而上建模方法,Paatero和Lund[10]根据季节和社会因素,将单个电器的启动建模为随机过程,利用两个主要数据集作为输入构建了一个两级模型:第一级定义了为每个家庭设置的家用设备以及总体负荷波动趋势,第二级借助最终使用的启动概率来模拟每个家庭中的每个电器。Stoke在[11]中提出了一个可以生成三种类型聚合负荷曲线模型:第一层根据相关负荷和电器数据归一化建模,得到普通家庭的30分钟需求曲线,第二层考虑到家庭收入、生活方式等得到指定住宅的30分钟需求曲线;第三层通过对启动概率建模来得到具有精细分辨率的选定家庭的1分钟需求曲线。Capasso等人[12]基于在意大利进行的使用时间调查,建模了单个电器的开始和持续时间,以及附加到每个电器的电力负载,通过汇总单个电器的消耗来建立住宅区的负荷曲线。Walker和Pokoski[13]对这一模型进行了改进,其人行为建模的基础是使用两种概率函数,分别称为可用性函数和倾向性函数,然后将其推广到Capasso等人的模型中。C. Sandels等人[14]利用马尔科夫链模拟办公人员在室状态,从而建立自下而上模型生成北欧具有代表性的办公楼用电负荷曲线。
从上述研究可以看出来,统计建模方法可以利用宏观经济、能源价格和收入以及其他区域或国家指标,更易于开发和使用,还不需要详细数据。但是这种方法并没有提供太多细节和灵活性,从而导致精度不够,而且需要大样本。另外,统计建模方法通常难以解释和调查用户行为的影响。显然,自下而上的方法虽然需要大量能够反映家电消费行为的数据,但预测精度很高。对于自下而上方法来说,其模型主要存在三方面的不同:对成员行为描述的详细程度、对影响电器负荷分布的电器数据描述详细程度以及所使用的随机方法。在现有的文献研究中,很少有人既考虑到成员行为的随机性又考虑到电器使用数据的随机性。因此,本文综合考虑到成员行为以及电器使用功率和概率情况,建立了基于马尔科夫链蒙特卡洛方法的自下而上电负荷曲线模型。
本文利用马尔科夫链蒙特卡洛方法,通过转移概率矩阵得到室内有效用电人数,建立了人员模型;结合统计调研数据,利用不同电器不同时刻不同功率的使用概率,建立了电器模型。通过自下而上的建模思想结合人员模型和电器模型,得到日负荷曲线分布。所建模型具有系统性和通用性,适用于需求侧管理以及智能电网研究。
1 办公建筑日负荷建模体系
对于办公建筑的电负荷来说,可以分为基础负荷和与人员行为有关的负荷,基础负荷即对应电器功率保持固定值或者呈一定周期变化。对于与人员有关的负荷来说,建筑内人的行为会影响到对应电器的使用情况,建筑内人行为具有较大的随机性,但是因为办公建筑内部人员具有相对固定的作息时间,所以人员行为又具有一定的规律性,因此结合人员行为构建办公建筑日负荷曲线模型具有重要意义。
本文的办公建筑日负荷曲线建模体系如图1所示,首先根据负荷特性将负荷分为与人员行为有关的负荷和基础负荷,进而找到对应的电器。对于基础电器来说,某确定时刻的功率即为额定功率。对于与人有关的电器来说,首先通过转移概率矩阵建立人员模型,得到有效使用电器的人数;然后,根据统计调研数据,得到电器在不同时刻不同功率的使用概率,据此建立电器模型。根据人员模型和电器模型获得单个电器的日负荷分布曲线,再叠加所有电器得到房间的日负荷曲线分布情况。
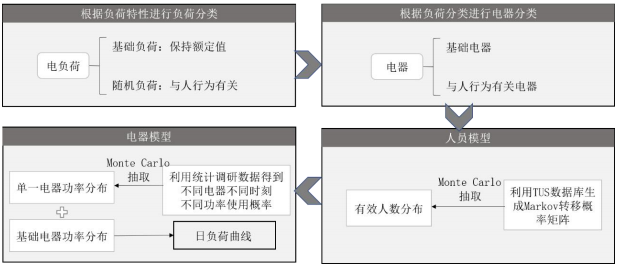
图1 基于马尔科夫链蒙特卡洛方法的自下而上办公建筑日负荷曲线建模体系
2 办公负荷人员模型
电器的使用情况并不是完全随机的,很大程度受到室内人员的影响。本文基于英国TUS(Time-Use Survey)数据库[15],利用马尔科夫链蒙特卡洛方法来生成有效用电人数。英国TUS 数据库对大量办公建筑进行调研,以15min为统计精度, 记录1天24 h活动日程,可以由此统计出1天内各时刻参与者的活动位置,得到建筑内的人员数量及其从事各种活动的概率。
2.1 MCMC方法
MCMC方法是一种特殊的蒙特卡洛方法,其将随机过程中的马尔科夫链应用于蒙特卡洛模拟中,抽样分布随模拟的进行而改变,从而实现动态模拟。
马尔科夫过程基于如下的思想:若随机过程在时刻ti 的状态已知,且在时刻t>ti 的状态仅与时刻ti的状态有关,而与ti前的状态无关,这个特性称为马尔科夫性或无后效性[16]。马尔科夫链模型基于状态转移矩阵( 即从某一状态转移到另一状态的概率) 建立,其中一阶马尔科夫链表示一个随机序列的条件概率只与前一时刻的系统状态有关, 而与之前的系统状态无关。其状态转移概率矩阵 P 如下所示:
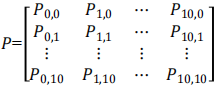 (1)
(1)
2.2 有效用电人数
建筑内电器的使用与有效用电人数密切相关,有效用电人数指的是某一时刻正在使用电器的人数。基于TUS数据库,每15分钟建立一个状态转移矩阵,考虑到某些房间可能人数较多,故房间人数分区间设置,分别为总人数的10%,20%...100%。利用MCMC方法仿真各时刻的有效人数nt如下公式:
nt=f(n,Pi,j,t) (2)
其中的n为总人数,Pi,j为转移概率,公式如下:
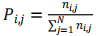 (3)
(3)
它表示由状态i转移到状态j的次数除以状态i的总转移次数,比如P1,2表示上一时刻的有效人数占比为0.1转移到下一时刻有效人数占比为0.2的概率。各时刻室内有效人数仿真流程如下图2:
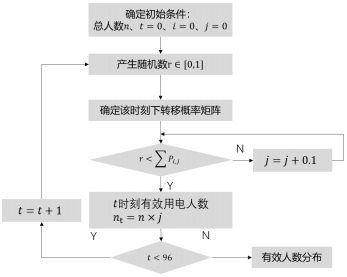
图2 有效人数生成的算法流程
(1)确定总人数n,初始时刻设置为0,初始状态设置为有效人数占比0;
(2)基于统计数据,利用MCMC方法,将生成的随机数与不同时刻转移概率矩阵的累计概率比较,确定不同时刻的有效人数;
(3)循环96次,得到有效人数在一天内的分布情况。
3 电器模型
由前述可知,办公建筑内的电器可以分为基础电器和与人有关的电器。基础电器的瞬时功率即为当前时刻的额定功率,计算公式如下:
Pb,T=Pe,T (3)
其中Pe,T为T时刻该电器的额定功率。
接下来主要讲述如何确定与人有关电器的瞬时功率值,计算流程如下图3所示:
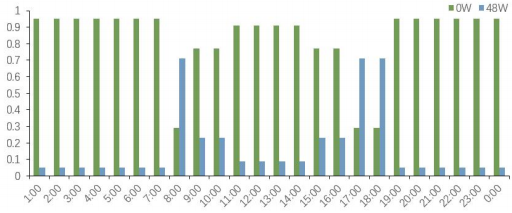
图3 与人有关电器的瞬时功率值计算流程
(1)根据统计数据,得到不同电器不同时间不同功率的使用概率,这里将设备的功率值按照实际情况分为不同的档数,假设为k档。
(2)利用随机数与累计概率比较,确定单台某电器在T时刻的功率如下公式:
 (4)
(4)
其中Lmk代表电器m在第k档的功率值,β为随机数,pT,i表示T时刻不同档位功率的概率。
(3)结合人员模型确定的有效用电人数,再引入共用系数α,得到T时刻某设备的功率如下公式:
Pm,T=Σanti=1Pm,s,i (5)
其中,nt为有效人数,i为进行蒙特卡洛抽取的次数,α为共用系数,反应电器共用情况,公式如下:
 (6)
(6)
其中A为同时使用人数。
(4)将这一过程循环M次就可以得到与人有关的设备总功率的瞬时值,公式如下:
Pp,T=ΣMm=1Pm,T (7)
其中M表示设备种类。
4、办公建筑日负荷曲线仿真
办公建筑的负荷特征由建筑内人员行为和开启的电器共同决定,结合人员模型和电器模型可以得到办公建筑日负荷曲线。
4.1 仿真结构
办公建筑日负荷曲线仿真结构如图4所示。结合人员模型和电器模型可以得到单个电器功率分布,进而得到所有与人有关的电器功率分布,再加上基础电器,将各时刻所有电器负荷曲线叠加即可获得日负荷曲线,日负荷瞬时值如下公式:
PT=Pb,T+Pp,T (8)
其中Pb,T为基础电器瞬时功率,Pb,T为与人有关电器瞬时功率。
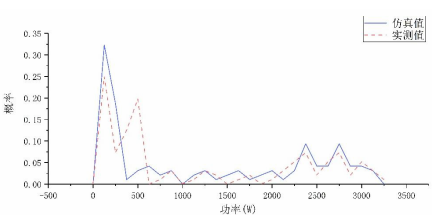
图4 办公建筑日负荷曲线仿真结构图
4.2 模型校验
4.2.1 案例介绍与模型数据来源
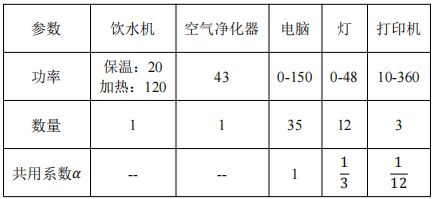
为了验证该办公建筑日负荷曲线模型的有效性,选取某行政办公楼的某一房间进行校验。该办公室共有35人,电器拥有情况为饮水机1台,空气净化器1台,电脑35台,灯12个,打印机3台。作息时间为9:00-17:00,周末休息。具体电器情况见下表1:
表1 办公室内电器情况

通过调研得知,打印机的工作功率为360W,不工作时的待机功率为10W;12盏灯采用“一开全开,一关全关”的状态,打开时功率为48W,关闭时为0,所以对于打印机和灯来说均为两档功率。对于电脑来说,通过实际调研发现其功率分布在0-150W之间,故每10W设置为一档位。对办公室内的电器进行为期一周的实际使用情况监测,每天每15分钟记录一次使用情况,从而得到不同电器不同时间段的使用情况。由于该办公楼为行政办公楼,加班情况较少但是也不排除,故结合国家统计局的相关数据资料,将非工作时间的电器使用概率均假设为0.05。由此,办公室内电器不同时刻不同功率的使用概率如下图5-7。
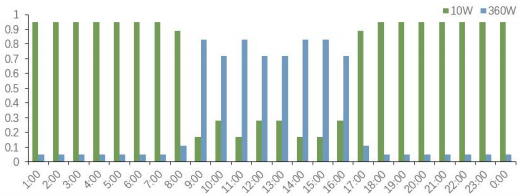
图5 打印机不同时刻不同功率使用概率

图6 灯不同时刻不同功率使用概率
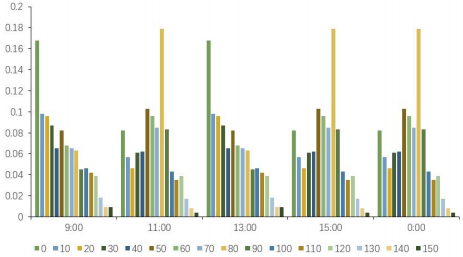
图7 电脑不同时刻不同功率使用概率
4.2.2 仿真结果与分析
根据前述办公室的信息,利用MCMC方法,得到的有效人数分布情况如下图8,从有效人数分布来看,上下午各有一个峰值,午休时间会有一个谷值,这是由于办公建筑的固定工作时间造成的,工作时间之外还考虑到一定的加班情况,故也有较少人数分布。
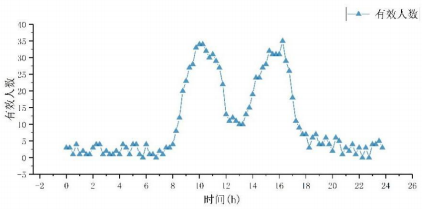
图8 有效人数分布情况
平均日负荷曲线通常用来作为选择配电系统元件容量的标准。故将一周5天工作日的模型数据与实测数据平均值作对比,以验证所建模型的有效性。图9是该办公室一周5个工作日的功率均值对比情况。由图9看出,模型结果与实测数据具有较好的相似性。
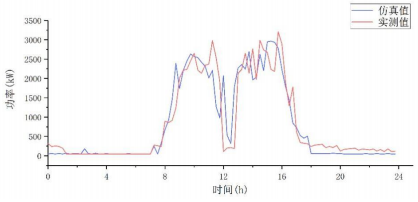
图9 该办公室日负荷均值仿真值与实测值对比
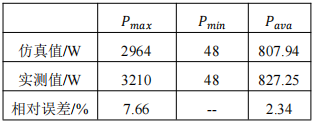
将5天内模型数据与实测数据的最大值、最小值及平均值作对比,以验证所建模型的有效性。如下表2所示,因为有一定的基础负荷昼夜保持运行,故最小值一致,对于最大值和平均值来说,最大相对误差为7.66%,在可接受范围内,仿真值与实测值具有较高一致性,故模型较为准确。
表2 电负荷最大值,最小值以及平均值的仿真值和实测值对比
该办公室一周5天工作日的概率密度曲线如图10所示。可以看出,实测值与仿真值的概率密度曲线具有良好的一致性。

图10 该办公室功率概率密度曲线仿真值与实测值对比
5 结论
本文基于统计调研数据,利用马尔科夫链蒙特卡洛方法建立了自下而上的办公建筑日负荷曲线模型。利用马尔科夫链蒙特卡洛方法建立人员模型得到有效使用电器人数;利用统计调研数据,确定不同电器不同时间不同功率的使用概率,据此建立电器模型。结合人员模型和电器模型得到日负荷分布情况。仿真与实测结果具有良好一致性,证实模型有效。该模型可以应用于需求侧管理、智能电网以及配电网动态研究,具有重要工程价值。
参考文献
[1] 王葵, 李建超, 潘贞存,等. 居民用户谐波调查及仿真分析[J]. 电力系统保护与控制, 2008(22):88-92.
[2] 黄海新, 邓丽, 文峰,等. 基于实时电价的用户用电响应行为研究[J]. 电力建设, 2016, 37(2):63-68.
[3] 朱海明. 电动汽车充电模式对主动配电网的影响[J]. 大科技, 2015, 36(028):97-102.
[4] Hoverstad, B.A.;Tidemann, A.;Langseth, H. Short-term load forecasting with seasonal decomposition using evolution for parameter tuning[J]. IEEE Trans. Smart Grid 2015(6):1904–1913.
[5] Chuan L ,Ukil A . Modeling and Validation of Electrical Load Profiling in Residential Buildings in Singapore[J]. IEEE Transactions on Power Systems, 2015, 30(5):2800-2809.
[6] Swan L G , Ugursal V I . Modeling of end-use energy consumption in the residential sector: A review of modeling techniques[J]. Renewable & Sustainable Energy Reviews, 2009, 13(8):1819-1835.
[7] Dordonnat V , Koopman S J , Ooms M , et al. An Hourly Periodic State Space Model for Modelling French National Electricity Load[J]. Tinbergen Institute Discussion Papers, 2008.
[8] [ Chi-hsiang Wang, Grozev G , Seo] S . Decomposition and statistical analysis for regional electricity demand forecasting[J]. Energy, 2012.
[9] Stephen B , Mutanen A J , Galloway S , et al. Enhanced Load Profiling for Residential Network Customers[J]. IEEE Transactions on Power Delivery, 2014, 29(1):88-96.
[10] Paatero J V , Lund P D . A model for generating household electricity load profiles[J]. International Journal of Energy Research, 2010, 30(5):273-290.
[11] Stokes M . Removing barriers to embedded generation : a fine-grained load model to support low voltage network performance analysis[J]. De Montfort University, 2005.
[12] Capasso A , Grattieri W . A bottom-up approach to residential load modeling[J]. IEEE Transactions on Power Systems, 1994, 9(2):957-964.
[13] Walker C F , Pokoski J L . Residential Load Shape Modeling Based on Customer Behavior[J]. IEEE Power Engineering Review, 1985, PER-5(7):34-34.
[14] Sandels C , Brodén, D, Widén, J, et al. Modeling office building consumer load with a combined physical and behavioral approach: Simulation and validation[J]. APPLIED ENERGY -BARKING THEN OXFORD-, 2016, 162:472-485.
[15] Milanovic J V , Yamashita K , Martinez Villanueva S , et al. International Industry Practice on Power System Load Modeling[J]. IEEE TRANSACTIONS ON POWER SYSTEMS PWRS, 2013, 28(3):3038-3046.
[16] Nijhuis M , Gibescu M , Cobben J F G . Bottom-up Markov Chain Monte Carlo approach for scenario based residential load modelling with publicly available data[J]. Energy & Buildings, 2016, 112.
备注:本文收录于《建筑环境与能源》2021年4月刊 总第42期(第二十届全国暖通空调模拟学术年会论文集)。版权归论文作者所有,任何形式转载请联系作者。















